Unidad 3 - MRUV, Caída Libre y lanzamientos verticales
- Hola chicos hoy vamos hablar sobre el Movimiento Rectilíneo Uniforme Variado, pero primero debemos saber sus características para reconocer que tipo de movimiento. Dentro de esta orden de ideas tiene una trayectoria rectilínea, ahora bien una rapidez o velocidad que varié en aumento. No hay que olvidarnos que su aceleración es constante y por ende es diferente a cero, no olvidemos que la ESCALAR SIEMPRE ES POSITIVA y por ultimo pero no menos importante sus vectores tienen la misma dirección o ángulos directores. Sus formulas son las siguientes:
d = Vo t + ½ a t2
Vm = d/t
Vf = Vo + a t
Vf2 = Vo2 + 2 a d
a = ΔV/ t
Este movimiento se cataloga en dos temas:
MOVIMIENTO RECTILÍNEO UNIFORMEMENTE VARIADO ACELERADO: MRUVA
- En función de lo planteado recordemos que este movimiento tiene trayectoria rectilínea, dicho de otro modo su rapidez o velocidad varía en aumento y se presenta con una aceleración que es constante. Cabe resaltar que es diferente de cero y su ESCALAR SIEMPRE VA SER POSITIVA, en este sentido se comprende que todos sus vectores , tienen la misma dirección o el mismo unitario, rumbo o ángulos directores.
MOVIMIENTO RECTILÍNEO UNIFORMEMENTE VARIADO DESACELERADO: MRUVD
- El análisis procedente es que su trayectoria es rectilínea, por consiguiente su rapidez o velocidad se varía en disminución. Dicho de otro modo su aceleración es constante y diferente de cero. Pero tenemos un dato muy importante aquí, que su ESCALAR ES NEGATIVA a diferencia del MRUVA, ahora bien sus vectores tienen la misma dirección o ángulos directores. Por último es conveniente acotar que el vector aceleración, tiene una dirección opuesta, unitario con signos contrarios a los vectores que hemos mencionado en el blog.
CAÍDA LIBRE
- En este movimiento es acelerado y por ende su rapidez va aumentando en cada segundo del movimiento, se observa que su aceleración es la gravedad 9,8m/s y el valor en vectorial es -9.8 j m/s². Por otra parte su rapidez inicial es igual a cero. Cabe considerar que todos sus vectores son negativos y están señalados en sistema de vectores base, esto significa que siempre van a tener el vector base j.
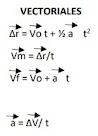
h = Vo. t + ½ g t
2
Vf = Vo + g t
Vm =
𝑉𝑓+𝑉𝑜/ 2
Vm =
𝑑/ 𝑡
Vf2 = Vo2
+ 2 g/ h
LANZAMIENTO VERTICAL HACIA ABAJO
- Dentro de esta orden de ideas el movimiento se lo identifica gracias al objeto que es impulsado y su trayectoria es vertical y hacia abajo desde una altura establecida, ahora bien contiene las mimas formulas que caída libre.
LANZAMIENTO VERTICAL HACIA ARRIBA
- En relación a este tema cuando el objeto sube MRUVD de dicho de otra manera su rapidez disminuye a cada segundo a razón de 9,8m/s se observa que cuando llega al punto más alto de su trayectoria la rapidez del objeto es igual a cero, se plantea entonces qué comienza a caer en movimiento rectilíneo uniforme variado acelerado y llega al suelo , con la misma rapidez que fue lanzado el objeto cuando comenzó el movimiento. Ahora bien el tiempo que tarda el objeto en subir hasta el punto más alto, es el mismo tiempo que tarda en caer y al regresar a la superficie.
DESDE CIERTO NIVEL DE ELEVACIÓN
- Dentro de esta orden de ideas, el tiempo que tarda el cuerpo en subir hasta el punto más alto, es menor que el tiempo que tardaría en caer y regresar a la superficie, ahora bien la suma del tiempo en subir más el tiempo en bajar nos da como resultado el tiempo de vuelo. Cabe señalar que la suma de la altura de el objeto más la altura de lanzamiento no das como resultado la altura máxima alcanzada por el objeto. Tomar en cuenta las características
- Uno de los componentes más importantes del movimiento parabólico es que está en el plano, debe señalarse que tiene una trayectoria parabólica, a diferencia de los movimientos anteriores. De esta manera su velocidad inicial es diferente a cero y no es vertical retomando la expresión del movimiento de parabólico tiene componentes en X de la velocidad inicial constante durante todo el movimiento. Se plantea entonces que el eje X es el objeto tiene MRU. Por consiguiente el eje Y del objeto tiene MRUV variado desacelerado cuando sube es acelerado pero cuando baja en este sentido se comprende que la aceleración de la gravedad influye en el movimiento.
Lanzamiento horizontal desde cierta altura
- Dentro de este orden de ideas el movimiento está en el plano, cabe resaltar que su lanzamiento es desde cierta altura. Dicho de otro modo su trayectoria es parabólica, se observa que su velocidad inicial es diferente a cero pero horizontal retomando la expresión de componente en X de la velocidad inicial constante durante todo el movimiento. Por consiguiente en el eje X el objeto tiene MRU ahora bien en el eje Y del objeto tiene MRUVA o sea caída libre, por último es conveniente acotar que la aceleración y la gravedad influye en el movimiento y el tiempo en creer constituye el tiempo de vuelo.
Lanzamiento parabólico desde el suelo
- Uno de los componentes más importantes es qué movimiento está en el plano y es lanzado desde el suelo por dichas razones su trayectoria es parabólica, en relación con este tema su velocidad inicial es diferente de cero por lo general el vector en el primer cuadrante .Se observa que el componente en X de la velocidad inicial es constante durante todo el movimiento, en relación con idea interior en el eje X el objeto tiene MRUy el eje Y del objeto tiene MRUVA cuando sube y en caída libre o sea cuando baja. Dentro de este marco su aceleración es la gravedad influye en el movimiento el tiempo subir es igual tiempo en bajar, dicho de otro modo el tiempo de vuelo es la suma del tiempo en subir más el tiempo de bajar.
Lanzamiento parabólico desde cierta altura
Se plantea entonces que este movimiento la altura máxima alcanzada se calcula como la suma de la distancia al subir más altura de lanzamiento esta altura constituye a la altura distancia recorrida cuando el objeto cae, que me resulta que todas las velocidades en el movimiento parabólico. Están expresadas como un vector en el plano, se plante entonces que este caso es un lanzamiento parabólico. Es un vector que pertenece al primer cuadrante cuando el objeto se encuentra sobre el nivel de lanzamiento retomando la expresión del cuarto cuadrante cuando el objeto se encuentra debajo del nivel de la de lanzamiento.




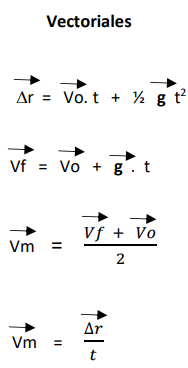







Comentarios
Publicar un comentario