Aprendamos sobre los vectores

el

Muchas veces no entendemos las clases de física ¿Por que?. Hay que darle una forma divertida de enseñar, y aquí te lo enseñaremos todo lo que necesitas saber sobre los vectores.



¿Qué son las magnitudes?


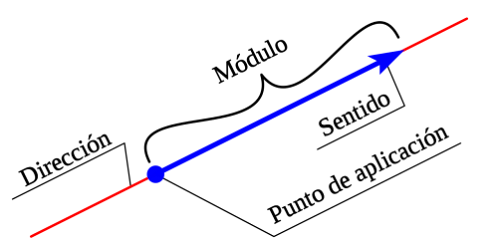
Dentro de la física se consideran dos magnitudes: Las magnitudes escalares que son      conocidas por su magnitud y su unidad correspondiente. Como por ejemplo la distancia, temperatura, tiempo, masa, etc. Y la magnitud vectorial es aquella que tiene un punto de aplicación, magnitud o modulo, sentido dirección 

¿Qué son los vectores?

Un vector podría ser representado gráficamente por medio de una flecha. Como sabemos  el vector puede estar localizado sobre un eje, un plano o en el espacio. Por consiguiente, para graficarlo, se usará un sistema de alusión o plano cartesiano. 
Hay que saber diferenciar las diferentes partes del vector igual mente saber sus definiciones como por ejemplo: Un punto de aplicaron es aquella que donde se origina el vector, la magnitud o modulo es el tamaño del vector que siempre va acompañado de su unidad correspondiente, el sentido nos indica hacia donde se dirige el vector  y la dirección hay que recordar que es el ángulo de la forma del vector, que va en sentido ANTIHORARIO desde el eje x positivo hasta llegar al vector. ¿ Muy fácil cierto?

Pero no olvidemos que si  la dirección de un vector esté comprendida entre 0 y 90°, el vector estará en el primer cuadrante, igualmente si la dirección del vector está comprendida entre 90° y 180°, el vector estará en el segundo cuadrante. Cuando la dirección es un ángulo comprendido entre 180° y 270°, el vector estará en el tercer cuadrante. Y si la dirección está comprendida entre 270° y 360°, el vector estará en el cuarto cuadrante.
OJO: recuerden que la dirección siempre es positiva 


Un vector puede ser representado o expresado en diferentes sistemas como: 

1. Sistema de coordenadas rectangulares
 2. Sistema de coordenadas polares
 3. Sistema de coordenadas geográficas 
4. Sistema de vectores base 
5 Sistema módulo y unitario
 6. Sistema módulo y ángulos directores 

 Recordamos en el blog Anterior sobre que eran los vectores y sus elementos.

Sabían que un vector en el plano, está expresado en este sistema, una vez que se conocen sus 2 componentes.

  • Si ambas componentes son positivas, el vector está en el primer cuadrante.  
  • Si la primera componente es negativa y la segunda positiva, el vector pertenece al segundo cuadrante. 
  • Si ambas componentes son negativas, el vector está en el tercer cuadrante.
  •  Si la primera componente es positiva pero la segunda es negativa, el vector pertenece al cuarto cuadrante.

CÁLCULO DEL MÓDULO DE UN VECTOR EN COORDENADAS RECTANGULARES

En primera instancia, el módulo de un vector continuamente va a ser una porción POSITIVA, que va acompañada de la unidad que corresponde.

                →
Formula: | A | = MÓDULO DEL VECTOR A

Para establecer el módulo de un vector que está expresado en el Sistema de coordenadas rectangulares


CÁLCULO DE LA DIRECCIÓN DE UN VECTOR EN SISTEMA DE COORDENADAS RECTANGULARES

  La dirección de un vector, como ya se señaló, es el ángulo que se mide a partir del eje X

 positivo en sentido antihorario hasta llegar al vector. Este ángulo cambia de consenso al

 cuadrante en el que está el vector

  • PRIMER CUADRANTE: 0 < Ꝋ < 90° 
  • SEGUNDO CUADRANTE: 90° < Ꝋ < 180° 
  • TERCER CUADRANTE: 180° < Ꝋ < 270° 
  • CUARTO CUADRANTE: 270° < Ꝋ < 360°
La dirección de un vector, como ya se indicó, es el ángulo que se mide desde el eje X positivo en sentido antihorario hasta llegar al vector. Este ángulo cambia de acuerdo al  cuadrante en el cual está el vector: 



Ojo: No olvidemos los signos
 

SISTEMA DE COORDENAS POLARES


Se identifica  en sistema de coordenadas polares cuando se conocen su Módulo y su Dirección. No debemos olvidarnos recordar que tanto el módulo como la dirección, siempre son cantidades positivas.


Para verificar en qué cuadrante se encuentra un vector expresado en Sistema de Coordenadas Polares

  • PRIMER CUADRANTE: 0 < Ꝋ < 90° 
  • SEGUNDO CUADRANTE: 90° < Ꝋ < 180° 
  • TERCER CUADRANTE: 180° < Ꝋ < 270° 
  • CUARTO CUADRANTE: 270° < Ꝋ < 360°
Para el cálculo de las componentes rectangulares de un vector expresado en el Sistema de Coordenadas polares

SISTEMA DE COORDENADAS GEOGRÁFICAS

En sistema de coordenadas geográficas se conoce su módulo y el rumbo del vector. El RUMBO es una forma de dirección del vector, pero NO es la verdadera dirección del vector.
Es distinguido por la expresión que utiliza los puntos cardinales: Norte, Sur, Este y Oeste

  • Si el vector se ubica en el primer cuadrante y se conoce el rumbo, se resta dicho rumbo de 90°
  • Si el vector se ubica en el segundo cuadrante y se conoce el rumbo, se suma dicho rumbo con 90°
  • Si el vector se ubica en el tercer cuadrante y se conoce el rumbo, se resta dicho rumbo de 270°
  • Si el vector se ubica en el cuarto cuadrante y se conoce el rumbo, se suma dicho rumbo con 270°

CÁLCULO DEL RUMBO CUANDO SE CONOCE LA DIRECCIÓN DEL VECTOR 

  • Si  el vector en el primer cuadrante, nos indica que la dirección debe ser menor a 90° y que los puntos cardinales serán Norte y Este
  • Si el vector en el segundo cuadrante, nos indica debe ser mayor que 90°, pero menor que 180° y que los puntos cardinales serán Norte y Oeste
  • Si el vector en el tercer cuadrante, nos indica que la dirección debe ser mayor que 180°, pero menor que 270° y que los puntos cardinales serán Sur y Oeste.
  • Si el vector en el cuarto cuadrante, nos indica que la dirección debe ser mayor que 270°, pero menor que 360° y que los puntos cardinales serán Sur y Este

Para realizar el cálculo de las componentes rectangulares de un vector expresado en el Sistema de Coordenadas Geográficas

SISTEMA DE VECTORES BASE 

Se reconocen sus componentes rectangulares y cada una de éstas, va acompañada del respectivo vector base. Ejemplos

Ojo: los elementos no permanecen separadas por un punto y coma, sino que permanecen expresadas de forma continua, como una expresión algebraica que pone de manifiesto los signos de dichas componentes. Esto nos indica esta expresión va entre paréntesis y fuera de los mismos, la unidad correspondiente del vector. 

Modulo:

     


Dirección:


 Cálculo del rumbo cuando se conoce la dirección del vector:

  • PRIMER CUADRANTE: 0 < Ꝋ < 90° 
  • SEGUNDO CUADRANTE: 90° < Ꝋ < 180° 
  • TERCER CUADRANTE: 180° < Ꝋ < 270° 
  • CUARTO CUADRANTE: 270° < Ꝋ < 360°

SISTEMA MÓDULO Y UNITARIO


Se reconoce cuando se conoce su Módulo y su unitario. Es el vector expresado en Sistema de Vectores Base, cuyas elementos son números decimales menores o equivalentes a uno.
 Este vector, no posee unidades. 
Símbolo µA

Para establecer a sistemas de vector Base 

Aplicamos  aplica la propiedad distributiva, y se multiplica el módulo del vector por cada componente del unitario del vector

Ojo se puede determinar sus componentes rectangulares y con éstas, podemos hallar la dirección y el rumbo del vector

Cálculo del Vector Unitario, cuando un vector está expresado en Sistema de Coordenadas Rectangulares

Si un vector está expresado en Sistema de Coordenadas Rectangulares, es aconsejable cambiar al vector al Sistema de Vectores Base. Después, el Vector Unitario del mismo.

Cálculo del Vector Unitario, cuando un vector está expresado en Sistema de Coordenadas Polares 


Cálculo del Vector Unitario, cuando un vector está expresado en Sistema de Coordenadas Módulo y Ángulos Directores 



SISTEMA MÓDULO Y ÁNGULOS DIRECTORES

Se diferencia por que se conoce su Módulo y los ángulos Directores del Vector. Módulo de un vector es la magnitud o longitud del vector. Ángulos Directores de un vector, son los ángulos que forma el vector con todos los ejes X, Y, Z positivos 
  • Ángulo Alfa: Es el MENOR ángulo tiene el vector con el eje X POSITIVO. 
  • Ángulo Beta: Es el MENOR ángulo que tiene el vector con el eje Y POSITIVO.
  •  Ángulo Gama: Es el MENOR ángulo que tiene el vector con el eje Z POSITIVO
Ángulos directores en el plano
  • Cuando los dos ángulos directores α y β de un vector, son agudos (menor a 90° ) , el vector se esta el I cuadrante. 
  • Cuando el ángulo director α es obtuso (mayor de 90° ) y el ángulo director β es agudo (menor de 90o°), el vector esta en el II cuadrante.
  • Cuando los dos ángulos directores α y β de un vector, son obtusos (mayor a 90°), el vector esta a en el III cuadrante.
  • Cuando el ángulo director α es agudo (menor de 90°) y el ángulo director β es obtuso (mayor de 90° ), el vector esta  en el IV cuadrante.

CÁLCULO DE LOS ÁNGULOS DIRECTORES CUANDO SE CONOCEN LAS COMPONENTES DE UN VECTOR:


SISTEMA ESPECIAL DE VECTORES EN EL ESPACIO

Se le identifica por su módulo, rumbo y además se menciona una depresión o elevación de dicho vector, entonces se trata de una magnitud vectorial en este sistema.
Primero se establece la elemento en Y del vector, multiplicando el módulo por el

 SENO del ÚLTIMO ÁNGULO expresado en este vector. Además, si dice Altura, el símbolo de dicha elemento en Y va a ser POSITIVA, empero si dice DEPRESIÓN, el símbolo de dicha
componente en Y va a ser NEGATIVA. En segundo sitio, se nace a establecer la elemento del plano XZ, multiplicando el módulo del vector por el COSENO del ÚLTIMO ÁNGULO expresado en este vector. Esta elemento Constantemente va a ser POSITIVA. Esta elemento XZ, va a servir de módulo para las próximas elementos X y Z. En tercer sitio, se establece la elemento en X del vector, multiplicando el resultado de la elemento XZ, por el COSENO de la DIRECCIÓN que se recibe del RUMBO.
 Finalmente, se establece la elemento en Y del vector, multiplicando el resultado de la elemento XZ, por el SENO de la DIRECCIÓN que se recibe del RUMBO, empero a este resultado Constantemente SE LE CAMBIA DE Símbolo. 

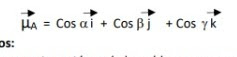
Comentarios

Publicar un comentario