Operaciones vectoriales y Cinemática

 Operaciones vectoriales y Cinemática 

Hola chicos hoy vamos aprender sobre las operaciones vectoriales y la cinemática . No se asusten que aquí van aprender que es divertido estudiar con Alexia. Manos a la obra!

Suma Vectorial 

Sabemos que la suma vectorial son entre dos o mas vectores y eso nos da como resultado otro vector. Pero recordemos que existen dos procedimientos que son el método analítico y el método grafico.

Método Analítico 

Debemos acotar que para sumar vectores por el método analítico es importante recordar que todos los vectores sumando deben estar expresados en el sistemas de coordenadas polares, rectangulares o vectores base. Ahora bien proseguimos con la suma de las componentes X, las componentes Y y por ultimo las componentes Z. De esta forma obtenemos el resultado de la suma vectorial

¿Muy fácil cierto? Pero nos falta un ejemplo para entender mejor!

Método Grafico 

Recordemos que todo método grafico nos ayuda a obtener resultados aproximados pero no exactos. Ahora bien existen el método paralelogramos y el método polígono. Aprendamos estos nuevos métodos!

Método paralelogramo

Debemos recordar que por este método es importante graficar un sistema de coordenadas en el centro de la hoja (OJO: Que sea papel milimetrado) Procedemos a graficar los dos vectores sumando. No te olvides de un compas, es muy necesario en este método 

Nosotros con el compas, medimos el vector (A), es necesario pinchar en el origen y abriendo el compas hasta el final del vector, en otras palabras su extremo. No perdamos la medida que obtenemos del primer vector ya que nos sirve para trasladar al extremo final del otro vector sumando (B), se pincha la punta de B y realizamos un arco con la abertura de A. Con el otro vector se mide (B) pinchando exactamente en el origen y abriendo el compas hasta el final del extremo de nuestro vector. Esta medida que obtenemos la trasladamos al extremo final del otro vector sumando (A), ahora bien pinchamos la punta de A y procedemos a realizar un arco con la abertura del vector B. Como podemos observar al realizar estos trazos se cortaran dos arcos en un punto. No olvidemos que con linea entre cortada se unira este punto con los extremos finales de nuestro vector A y B. Y así chicos obtenemos un paralelogramo que su diagonal es el resultado de la suma A y B

Un ejemplo nos podrá ayudara a comprender mejor!

Método Polígono

Recordemos que podemos sumar dos o mas vectores por este método. Comenzamos trazando el primer sistema de referencia por el cual se dibuja el primer vector sumando, posteriormente en la punta del primer vector, trazamos un nuevo sistema de referencia y en el segundo sistema, graficamos el segundo vector sumando. En la saeta de este segundo vector, nuevamente trazamos un sistema de referencia, por ende en el tercer sistema se grafica un tercer vector sumando. Por ultimo trazamos el ultimo vector en el origen del primer sistema de coordenadas con el extremo final del ultimo vector sumando. (OJO recordemos que el modulo se mide con la ayuda de una regla con el graduador expresamos el resultado del vector)

No olvidemos que vamos obtener resultados aproximados, Por ejemplo 

Producto de un escalar por un vector 

Debemos acotar que para esta operación necesitamos que el vector está expresado en un sistema de vectores base o rectangulares, por consiguiente se multiplica el escalar o un número por el vector, aplicamos la propiedad distributiva y se obtiene un resultado qué es un vector nuevo

Producto punto 

Primero reconozcamos cual es su símbolo
 

Para ejecutar esta operación necesitamos transformar cada vector al sistema de vectores base rectangulares. Procedemos a multiplicar entre si, las X. las Y por último las Z. vamos a obtener tres números como resultados de estas multiplicaciones. Por ultimo vamos a sumar estas tres respuestas obteniendo el resultado final de esta operación.

El ejemplo nos ayudara a comprender mejor !

Producto Cruz

Aprendamos cual es su signo 

Debemos recordar que esta operación se realiza entre dos vectores y es una multiplicación, que  vamos a obtener que el resultado es otro vector. OJO chicos también se le conoce como Producto vectorial. Para desempeñar esta operación, es imprescindible transformar cada vector a sistemas de vectores base o rectangulares. Ahora bien se procede a resolver un determinante de 3* 3 el cuál será la primera fila siempre estará conformada por las tres bases (i, j, k ) por ende la segunda fila del determinante estará formada por los componentes del primer factor, y por último la tercera fila por las componentes el segundo vector Factor 

Resolvemos esta operación y vamos a obtener el resultado final

Los ejemplos nunca van a faltar en este blog

Ángulo entre dos vectores

Memoricemos cual es su formula

Cuándo obtenemos el producto punto de los dos vectores, al resultado se divide para el producto de los dos módulos de nuestros dos vectores aplicando la función que ya aprendimos

Wow que rápido aprendemos juntos! Aquí va el siguiente ejemplo 

Proyección de un vector sobre otro vector

Debemos recordar cual es su formula

Debe señalarse que se encuentra el producto punto entre el primer vector y el vector unitario del segundo vector, así obtendremos el resultado que es un número. Ahora bien se multiplica por el unitario del segundo vector y el resultado es vector proyección de A sobre B.

Nuestro ejemplo nunca debe faltar

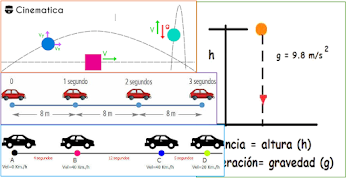
Cinemática 

El MRU se define el movimiento en el cual un objeto se desplaza en línea recta, en una sola dirección, recorriendo distancias iguales en el mismo intervalo de tiempo, manteniendo en todo su movimiento una velocidad constante y sin aceleración. En este movimiento recordemos que  todos los vectores, tienen la misma dirección, ángulos directores, rumbo o unitario.